Wilcoxon Signed Rank Test Continuity Correction
Wilcoxon Signed-Ranks Test for Paired Samples
When the requirements for the t-test for two paired samples are not satisfied, the Wilcoxon Signed-Rank Test for Paired Samples non-parametric test can often be used.
In particular, we assume n subjects from a given population with two observations xi and y i for each subject i. This results in two paired samples {x 1,…,xn } and {y1,…,y n } as described in Paired Sample t Test. The requirements for the Wilcoxon Signed-Rank Tests for Paired Samples where zi = y i – xi for all i = 1, … , n, are as follows:
-
- the zi are independent
- xi and y i are interval data (and so a ranking can be applied and differences can be taken)
- The distribution of thezi is symmetric (or at least not very skewed)
If the second or third assumption is violated, then you should consider using the Sign Test, which doesn't require symmetry.
For this test we use the following null hypothesis:
H0: the distribution of difference scores in the population is symmetric about zero
I.e. any differences are due to chance. We show how to apply this test via a couple of examples.
Examples
Example 1: A researcher wanted to determine whether people's ability to identify objects with their right eye differs from their ability with their left eye. 16 subjects were presented with a series of images and were scored on their abilities to identify objects which each eye. The results are tabulated in Figure 1. Based on this data, use the Wilcoxon Signed-Ranks Test to determine whether there is a difference between the two eyes.

Figure 1 – Wilcoxon Signed-Ranks Test for Paired Samples
We perform a two-tailed Wilcoxon Signed-Ranks Test for Paired Samples with α = .05 to test the following null hypothesis:
H0: any differences between the two eyes is due to chance (essentially based on the median of the differences)
The scores for the two eyes are presented in columns B and C. Column D contains the differences between the scores for each subject. Column E contains the absolute value of these differences, eliminating any zero differences from further consideration. Column F contains the adjusted rankings of the non-zero values in column E. Column G reports the values in column F where the difference in column D is positive. Column H reports the values in column F where the difference in column D is negative.
Columns G and H are summed (in cells G19 and H19) to obtain T+ of 69.5 and T- of 35.5. The smaller of these values is the test statistic T = 35.5 (in cell K7).
The critical values for the T statistic are given in the Wilcoxon Signed-Ranks Table. Here we use α = .05 and n = 14 (i.e. the 15 subjects less the 1 subject where the difference value in column D is zero). From the table, we find that Tcrit= 21 (two-tail test). Since Tcrit = 21 < 35.5 = T, we can't reject the null hypothesis (i.e. p ≥ .05), and so conclude there is no significant difference between the two eyes.
Normal Approximation
Generally, for n > 25, an estimate using the normal distribution can be made (as seen in the next example). The actual threshold of 25 is not universally accepted and can be lowered to around 15 or raised to about 50.
Property 1: Whenn is sufficiently large, the T statistic (or even T+ or T-) has an approximately normal distribution N(μ, σ) where
![]()
Click here for a proof of Property 1.
Correction for Ties
Property 2: If there are a large number of ties, a better estimate of the variance is given by
![]()
where t varies over the set of tied ranks and ft is the number of times (i.e. frequency) that the rank t appears.
Continuity Correction
It is often desirable to account for the fact that we are approximating a discrete distribution via a continuous one by applying a continuity correction. This is done by using a z-score of
![]()
instead of the same formula without the .5 continuity correction factor.
Example 2: A study is made to determine whether there is a difference between husbands' and wives' attitudes towards politics. A questionnaire measuring this was given to 30 couples with the results summarized in range A3:C33 of Figure 2. Determine whether there is a significant difference between a couple's attitudes towards politics (without using a ties or continuity correction).
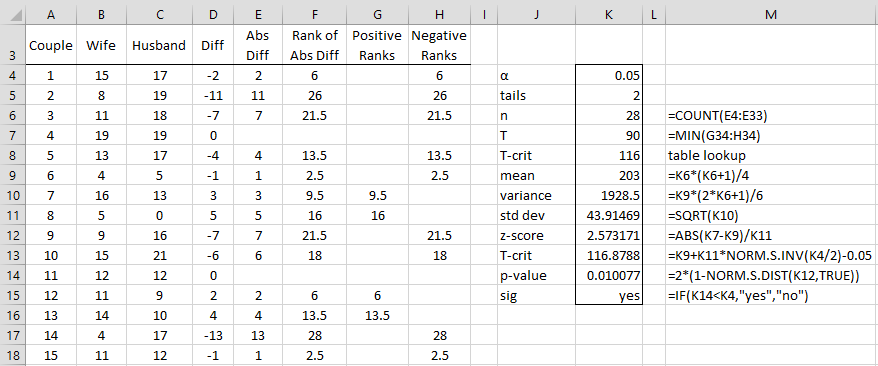
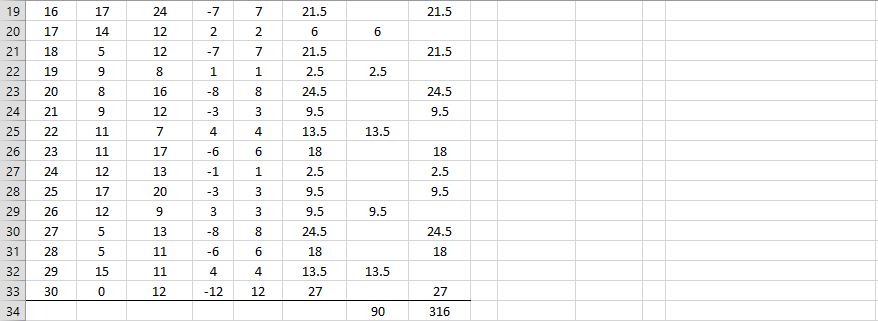
Figure 2 – Wilcoxon Signed-Ranks Test for Paired Samples
The figure is similar to that in Figure 1. Since T = 90 < 98 = Tcrit (two-tail test), we conclude there is a significant difference between a husband and his wife's attitude to politics.
Alternatively, we can conduct the analysis using the normal distribution approximation, as we did in Example 2 of Mann-Whitney Test. This time, we calculate a mean of 203 (cell K9), a variance of 1928.5 (cell K10) and a standard deviation of 43.9 (cell K11). From these, we calculate a z-score of 2.57 (cell K12), which yields a p-value (cell K14) of .01 (two-tail test), which is less than α = .05, and so once again we reject the null hypothesis. Note too that Tcrit = 116.8788 (cell K13), is based on the normal approximation and not a table lookup.
Worksheet Functions
Real Statistics Excel Functions: The following functions are provided in the Real Statistics Pack:
SRANK(R1, R2) = T for a pair of samples contained in ranges R1 and R2, where both R1 and R2 have only one column. R1 and R2 must have the same number of elements.
SRTEST(R1, R2, tails, ties, cont) = p-value for the Signed-Ranks test using the normal distribution approximation for the pair of samples contained in ranges R1 and R2, where both R1 and R2 have only one column. R1 and R2 must have the same number of elements.tails = 1 or 2 (default); if ties = TRUE (default) then a ties correction is used; if cont = TRUE (default) then a continuity correction is used.
There are also versions of SRANK and SRTEST which take only one range R1, which consists of two columns, one for each paired sample.
SRANK(R1) = T for a pair of samples contained in range R1, where R1 consists of two columns, one for each paired sample.
SRTEST(R1,,tails, ties, cont) = p-value for the Signed-Ranks Test using the normal distribution approximation.
These functions ignore any empty or non-numeric cells.
Observation: In Example 2, SRANK(B4:C33) = 90, which is the same as the T value shown in cell K7 of Figure 2. The two-tailed p-value (assuming the normal approximation), shown in cell K14, can also be calculated by the formula SRTEST(B4:C33,2,FALSE,FALSE) = 0.010077. We can also use the two-argument versions of these functions, namely SRANK(B4:B33,C4:C33) and SRTEST(B4:B33, C4:C33,2,FALSE,FALSE).
Effect Size
As for the Mann-Whitney test for independent samples, we can use the correlation coefficient r as a measure of effect size where
![]()
Here 2n = the number of observations, including the cases where the difference is 0. For Example 2
![]()
which represents a medium-sized effect.
More Worksheet Functions
Real Statistics Function: The Real Statistics Pack also provides the following array function for the samples in ranges R1 and R2. The output includes three different estimates of the p-value of the signed-ranks test, namely based on the normal approximation, the exact test and the simulation test. The last two of the tests will be described at the end of this webpage.
SR_TEST(R1, R2, lab, tails, ties, cont, exact, iter): returns the following values in a 6 × 1 column array: T-stat, z-stat, r effect size and the three types of p-values. If ties = TRUE (default), the ties correction is applied. If cont = TRUE (default) then the continuity correction is applied. If lab = TRUE (default FALSE) then an extra column with labels is included in the output.
If exact = TRUE (default FALSE) or if the size of each sample is less than or equal to 500, then the p-value of the exact test is output and if iter ≠ 0 then the p-value of the simulation version of the test is output where the simulation consists of iter samples (default 10,000).
Once again, the R2 argument can be omitted if R1 contains two columns (one for each sample). The exact and simulation versions of the test are described subsequently.
For Example 2, the array formula
=SR_TEST(B4:B33,C4:C33,TRUE,,FALSE,FALSE)
returns the array shown in Figure 3:

Figure 3 – Output from SR_TEST for paired samples
Data Analysis Tool
Real Statistics Data Analysis Tool: The Real Statistics Resource Pack also provides a data analysis tool that performs the Wilcoxon signed-ranks test for paired samples, automatically calculating the medians, T test statistic, z-score, p-values and effect sizer.
For example, to use this data analysis tool for Example 2, press Ctrl-m and choose T Tests and Non-parametric Equivalents from the menu that is displayed (or from the Misc tab if using the Multipage user interface). A dialog box will appear as shown in Figure 3 in Mann-Whitney Test for Independent Sample. Enter B3:C33 in the Input Range, check Column headings included with data, choose the Paired samples and Non-parametric options and make sure that all the Non-parametric test options are checked.
When you click on the OK button the output shown in Figure 4 is displayed.

Figure 4 – Wilcoxon signed-ranks data analysis for paired samples
Note that rows 16 through 20 of the figure show the results of the Wilcoxon signed-ranks test using the normal approximation, while the bottom two rows show the p-values of the test using the exact test and simulation respectively.
Since Use ties correction is checked, the ties correction defined by Property 2 is applied in the calculation of the standard deviation (cell U17 of Figure 4) as follows.
=SQRT(U16*(2*U10+1)/6)-TiesCorrection(B4:B33,C4:C33,1)/48
where the TiesCorrection function is as described in Mann-Whitney Test.
Since the Use continuity correction is checked, the 1/2 continuity correction is applied in the calculation of the z-score (cell U18) as follows:
=ABS(ABS(U13-U16)-1/2)/U17
Finally, note that the test ignores any data pairs where one or both of the values is non-numeric. The only exception to this is that the median values (U7 and V7 in Figure 4) are calculated separately, and so may include data that is not included in the test (since one of the elements in the pair is non-numeric).
Wilcoxon Signed-Ranks Test for a Single Sample
We can also use the Wilcoxon Signed-Ranks Test to test the following single sample null hypothesis:
H0: the median of the population is some given valuev
The approach we use is to apply the Wilcoxon Signed-Ranks test for paired samples, as described above, on a single sample {x 1,…,xn } where we assume the second sample consists ofn values all of which are v. The assumptions for this test are similar to those of the paired test, namely
- The xi are independent
- The xi are interval data (so that ranking can be applied and differences taken)
- The distribution of the xi is symmetric (or at least not very skewed)
If the second or third assumption is violated, you should consider using the Sign Test.
Worksheet Functions
Real Statistics Excel Functions: The following functions are provided in the Real Statistics Pack:
SRANK(R1, med) = T for a single sample contained in range R1 less med.If the second argument is omitted it defaults to zero.
SRTEST(R1, med, tails) = p-value for the Signed-Ranks test using the normal distribution approximation for the sample contained in range R1 less n. If the second argument is omitted it defaults to zero.tails = # of tails: 1 (default) or 2.
These functions ignore any empty or non-numeric cells.
Examples
Example 3: Determine whether the memory loss program described in Example 1 of the Sign Test is effective using a two-tailed Wilcoxon Signed-Ranks Test.
We repeat the data from this example in column B of Figure 5.
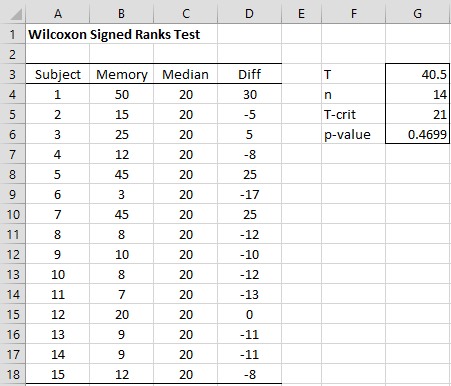
Figure 5 – Wilcoxon Signed-Ranks Test for a Single Sample
As shown in Figure 5, the memory data values are compared with the hypothetical median of 20%. We calculate T to be 40.5 (cell G3) using the formula SRANK(D4:D18) and find the critical value for T when n = 14 to be 21 (two-tail test) from the Wilcoxon Signed-Ranks Table. Since 40.5 > 21, we cannot reject the null hypothesis and conclude once again that there is no significant difference between the median of the data and 20%.
Using the normal distribution approximation, we see that SRTEST(B4:B18,20) = SRTEST(D4:D18) = .225629 > .05 = α, and so again conclude there is no significant difference between the median of the data and 20% (one-tail test).
Note that one way to calculate that n = 14 (cell G4) is to use the formula:
=COUNTIF(B4:B18,"<>"&20).
More Worksheet Functions
Real Statistics Function: The Real Statistics Pack also provides the following array function for the sample in range R1 where medis the hypothesized median (default = 0). The output includes three different estimates of the p-value of the signed-ranks test, namely based on the normal approximation, the exact test and the simulation test. The last two of the tests will be described at the end of this webpage.
SR_TEST(R1, med, lab, tails, ties, cont, exact, iter): returns the following values in a 6 × 1 column array: T-stat, z-stat, r effect size and the three types of p-values. If ties = TRUE (default), the ties correction is applied. If cont = TRUE (default) then the continuity correction is applied. If lab = TRUE (default FALSE) then an extra column with labels is included in the output.
If exact = TRUE (default FALSE) or if the size of each sample is less than or equal to 500, then the p-value of the exact test is output and if iter ≠ 0 then the p-value of the simulation version of the test is output where the simulation consists of samples (default 10,000).
For Example 3, the array formula =SR_TEST(B4:B18,C4,TRUE,,FALSE) returns the array displayed in Figure 6 (two-tailed test):

Figure 6 – Output from SR_TEST for a single sample
Data Analysis Tool
Real Statistics Data Analysis Tool: The Real Statistics Resource Pack also provides a data analysis tool that performs the Wilcoxon Signed-ranks Test for one sample, automatically calculating the observed median,T test statistic, z-score, p-values and effect sizer.
For example, to use this data analysis tool for Example 3, pressCtrl-m and chooseT Tests and Non-parametric Equivalents from the menu that is displayed (or the Misc tab if using the MultiPage user interface). A dialog box will appear as in Figure 3 in Mann-Whitney Test for Independent Sample. Enter B3:B18 in theInput Range, checkColumn headings included with data and enter 20 for the Hypothetical Mean/Mean. Next select theNon-parametric and Single sample options and make sure that all the Non-parametric test options are checked.
When you click on the OK button, the output shown in Figure 7 is displayed.

Figure 7 – Wilcoxon Signed-Ranks analysis for a single sample
Note that rows 14 through 18 show the results of the Wilcoxon signed-ranks test using the normal approximation, while the bottom two rows show the p-values of the test using the exact test and simulation respectively.
Since Use ties correction is checked, the ties correction is applied in the calculation of the standard deviation (cell AB15) as follows.
=SQRT(AB14*(2*AB8+1)/6-TiesCorrection(B4:B18,AB6)/48)
where the TiesCorrection function is as described in Mann-Whitney Test.
Since the Use continuity correction is checked, the 1/2 continuity correction is applied in the calculation of the z-score (cell AB16) as follows:
=ABS(ABS(AB11-AB14)-1/2)/AB15
Exact Test
Click here for a description of the exact version of the Signed Ranks Test using the permutation function.
Simulation
Click here for a description of how to use simulation to determine the p-value for the Signed-Ranks test. This approach takes ties into account.
Confidence Interval of the Median
Click here for a description of how to calculate a confidence interval of the median based on the Wilcoxon Signed Ranks Test.
Statistical Power and Sample Size
Click here for a description of how to calculate the power or minimum sample size of the Wilcoxon Signed Ranks Test.
Source: https://www.real-statistics.com/non-parametric-tests/wilcoxon-signed-ranks-test/
0 Response to "Wilcoxon Signed Rank Test Continuity Correction"
Enregistrer un commentaire